The CR analogue of Yau uniformization conjecture states that any complete noncompact Sasakian manifold of positive CR holomorphic bisectional curvature is CR biholomorphic to the standard Heisenberg group. In this talk, we affirm the partial result of the above conjecture on Sasakian manifolds by using Sasaki-Ricci flow. More precisely, we show that a complete noncompact Sasakian manifold
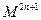 of nonnegative and bounded transversal bisectional curature with maximal volume growth is CR biholomorphic to
of nonnegative and bounded transversal bisectional curature with maximal volume growth is CR biholomorphic to
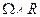 , where
, where
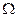 is a pseudoconvex domain of
is a pseudoconvex domain of
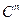 .
.











